The Additive Inverse
- Nicholas Gledhill
- Apr 8, 2024
- 3 min read
Updated: May 20, 2024
For every point P, on an Elliptic Curve, there exists a point P' (often denoted -P) for which P + P' = P + (-P) = P - P = the point at infinity.
The Inverse of the Inverse
Clearly, the opposite applies. That is:
- ( -P ) = P
Characteristic of 2 and 3
It should also be noted that an Elliptic Curve defined on any field of characteristic other than 2 or 3, can be converted into the Weierstrass form.
Weierstrass form and symmetry around the x-axis
The graph of an elliptic curve in Weierstrass form (Washington, L. C., 2008, pp9-11, Section 2.1), which is typically given by the equation:
y^2 = x^3 + Ax + B
(where A and B are constants in the equation), exhibits symmetry across the x-axis, due to several inherent properties of the equation and its geometric interpretation:
Equation Form: The equation y^2 = x^3 + Ax + B inherently defines symmetry about the x-axis because if (x,y) is a point on the curve, then (x,−y) must also be a point on the curve. This follows directly from the equation as squaring y and −y yields the same result, y^2.
Even Function: The function y = x^2 is an even function, meaning that its graph is symmetric with respect to the y-axis. In the context of the elliptic curve, this means that for every positive y value that satisfies the equation for a given x, there is a corresponding negative y value that also satisfies the equation. That is: if you "swap" the x and y, in y = x^2, you essentially get y^2 = f(x) - which is an elliptic curve, when f(x) is a cubic function of x.
Geometric Interpretation: Geometrically, the symmetry about the x-axis means that the curve mirrors itself across the x-axis. Any vertical line drawn at any x value on the curve will intersect the curve at points equidistant from the x-axis but on opposite sides.
Group Structure: The symmetry also plays a critical role in the group structure on the elliptic curve, particularly in the definition of the addition operation. When adding points on the elliptic curve (in the Weierstrass form), the symmetry about the x-axis is used to define the inverse of a point (x,y) as (x,−y), which is essential for ensuring that the curve forms an abelian group. This, coupled with the fact that any elliptic curve with a characteristic other than 2 or 3 can be converted into the Weierstrass form, allows us to use the symmetrical nature of the Weierstrass form for most investigations of the properties of an elliptic curve.
In summary, the symmetry of the elliptic curve in Weierstrass form about the x-axis is a direct consequence of the algebraic form of the equation, which specifies that the y-values are squared, thereby ensuring that both y and −y are solutions for any given x. This symmetry is crucial for the algebraic structure and the geometric properties of the curve.
The General Equation
Less obviously, the same rule of finding the inverse by vertical line projection also applies to the some more general equations for Elliptic Curves.
Some General Curve Forms
The "general form" of an elliptic curve might look like: y^2 + a_1xy + a_3y = x^3 + a_2x^2 + a_4x + a_6 (Washington, L. C., 2008, p10, Equation 2.1) - where a_1... a_6 are constants.
Given: P = (x,y)
Inverse (−P ): The inverse should maintain the curve's symmetry if it involves y^2. More generally, −P = (x , −y − a_1x − a_3). This adjustment accounts for the linear terms in y - but still defines a point vertically adjacent to P.
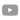
In the animation above, A and B (i.e. the basic form of the Weierstrass form of the equation) are kept the same - so all versions of the above Elliptic Curve can be converted to:
y^2 = x^3 + Ax + B
where A and B are constant.
We then substitute the values:
x_new = dx + f, and
y_new = ax_new + by + c
The animation above is an exploration of what happens to the general (new, transformed) equation, as you alter the values of d, f, a, b, and c - while A, B, and the initial equivalent values for P and Q (and the therefore R and R' = -R ) remain the same.